I/D 4: Unit V

During the activities in class, we discussed  how the shapes would all fit into the graph. We think that if all of the shape is given, maybe we could fit it into the graph like a puzzle piece. For a perfectly shaped graph, it was easier to solve because the shape fit nicely into it. However, on other graphs, it is harder because the shape is not porportioned . In order to solve for the ones that are not perfect, we would have to estimate it by putting pieces subtract it by the amount that is not used. In addition to, we also look at the scale of the graph. To do that, can figure out an estimate by figuring out the area of each space. It will give you a good estimate of the area.  In conclusion, we think that the most accurate graph use is to fit the pieces of shape on to the graph and estimate. As for the area, we think that you can estimate by looking at the scale of the graph alone.

BQ #6: Unit U

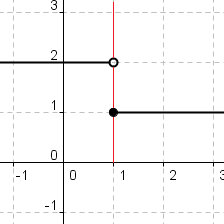
1. A continuity is a function that is very predictable because it has no breaks, no holes, and no jumps. It can be drawn without lighting up a pencil, in a single, unbroken line. A continuity is in the removable discontinuity called the point discontinuity. On the other hand, a discontinuity is has all of the opposite characteristic of the continuity. It has a break, hole, and jump. The discontinuity is put into the categories of non-removable discontinuity. Types of non removable discontinuities are jump discontinuity, oscillating behavior, and infinite discontinuity. A jump discontinuity has is different from left/right and has a break between the lines. An  oscillating behavior is wiggly while infinite discontinuity has a vertical asymptote and unbounded behavior.

Point Continuity

Oscillating Behavior

Jump Discontinuity

Infinite Discontinuity

2. A limit is the intended height of a function. It exist when there is an open hole on the graph. It is not the actual height but the intended height that it is trying to reach. The limit exist only when you reach the same height from both the left and right. A limit does not exist when there is a break in between the lines. For example in the jump discontinuity, a limit doe snot exist because it reaches two different places from left and right. A limit does not exist in the non removable discontinuities such as jump discontinuity, oscillating behavior, and infinite discontinuity. There is also a difference between the limit and value. A limit is the intended height while the value is the actual height. A value is represented by a closed circle.

Limits (intended height)

3. To evaluate the function numerically you have to set up the table and list the x value that is close to the number from left to right. You plug the equation onto the graphing calculator and trace the value. The y value will get closer and closer to the number therefore you can make ab educated guess of what the value is going to be. To evaluate it graphically you use your two finger and trace it from left to right. If the graph has a break then there is going to be a non removable type of discontinuity. To evaluate it numerically you first has to determine which kind of evaluation you're going to use. First. Start by using direct substitution. If it does not work you can determine it by using dividing out method, rationalizing, or limits at infinity

Limits Graphically

Limits Numerically

Credit/Disclaimer
Web Charter
Sage Math
All Math
Bakefield College
Khan Academy

BQ #4: WHy is a "normal" tangent graph uphill, ut a "normal" tangent graph downhill?

An asymptote will occur in the graph if the triq function is undefined. It is undefined when x is equal to zero. Tangent is Y/X. The tangent graph will have an asymptote at some point when x is zero. The reason why tangent graph is uphill and some are downhill is because it follows the ASTC. In a tangent graph, Q1=positive, Q2=negative, Q3=positive and Q4=negative.

 It will go up/down depending on the asymptote. Cotangent graph will have a similar graph. It will still follow the ASTC however, cotangent and tangent have a different location of asymptote. Since cotangent is x/y, the asymptote will start at a different place. Boundaries in different place will lead to the graph to be uphill/downhill.

BQ #3: How do the graphs of sine and cosine relate to eatch of the others?

Sine and Cosine relates to Tangent whenever Cosine/X is equal to zero. It happens to be where the curve on the graph is at. The curve is based on the ASTC of Tangent. Therefore, it will have different curves depending on the ASTC.

Cotangent will have an asymptote whenever sine is equal to zero. When sine is equal to zero, you will have undefined answer, therefore have an asymptote. The graph is uphill/downhill depending on where the asymptote is placed at. In this situtation, asymptote is located at 0, Pi, and 2pi.

Secant is the reciprocal of cosine. Secant will have an asymptote whenever cosine is equal to zero. The asymptote will be at pi/2, 3pi/2. On the first curve, it goes up next to the asymptote because the recicprocal of a fraction will make the number big, therefore will have to increased the curve. The curve will touch the "mountain" based on ASTC however, it will never touch the asymptote.

Cosecant will have an asymptote whenever sine is equal to zero because cosecant is the reciprocal of sine. Sine is zero at 0, pi, 2pi. The curve will depend on the ASTC of Sine. Sine is positive in qudrant 1,2. Because of that, the graph will be above the x asix. In qudrant 3,4 sine is negative. The graph will be below the x axix and will get close to the asymptote.

BQ #5: Why Do Sine and Cosine not have Asymptote, but the other four triq graphs do??

Sine and Cosine not have asymptote because it will never be undefined. The triq function of sine is y/r and cosine x/r. Since r=1, sine and cosine will be never undefined.

 As for the other triq functions, it does have an asymptote because the x, y could equal to zero. Therefore, the triq value of these functions will be undefined. Undefined triq functions will always have an asymptote on the graph.

BQ #2: How do the Triq Graphs Relate to the United Circle?

A. Period? Why is the peirod for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

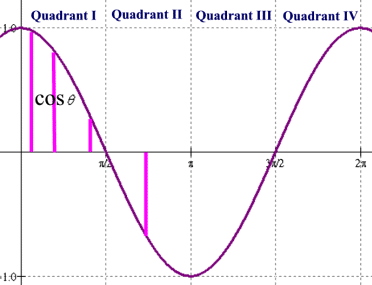
A period is the end and beginning of a cycle. It ends and starts when there is a repeating patterns. In this case. the reason why sine and cosine is 2 pi is because the pattern repeat itself fully around the Unit CIrcle. For tangent/cotangent, the pattern repeats only half way. For example in quadrant 1, tangent is positive, qudrant II negative, qudrant III positive, and quadrant IV negative. Therefore, it repeat itself only half of the graph.

Below are the sign for the triq function. The patterns can be seen by looking at the sign from Qudrant I to Qudrant IV.

The graph below also demonstrates how the triq function of sine and cosine relates to the unit circle. It marks the period of a cycle of a pattern. It would take 2pi for sine and cosine to repeat.

B. How does the fact that sine and cosine have amplitudes of one (and the other triq functions don't have amplitudes) relate to what we know about the Unit Circle?

IT relates to what we  know about the Unit Circle because sine is between 1 and -1 while cosine is between -1 and 1. Therefore, there is no restriction for the other triq function.

Photo Credit/Disclaimer

Reflection#1: verifying triq function

24. Verifying is basically like a proof in geometry. You have to prove that the answer is proven true by solving. The differences between verifying identities and proof is that we have to use the identities to prove that something is true. 

25. Some tips and trick I think is help ful include listing all the steps and go through it one by one when you don't know where to start. Also it is important to do it carefully and not make simple mistake such as distributing negative.

26. The first step into verifying a triq function is to look at the problem that they give you. For example,You can tell if you have to foil if the function has a parenthesis. Another would be if you have a fraction. You can find the common denominator and solve. From there you have to use the identity and the basic rule of math to verify your function. The big key here is substitution. You have to use identity to prove/solve the triq function in order to simplify it to 1 function.

SP7: Unit Q Concept 2- Finding Trig Function When Given One Trig Function and Quadrant

This SP7 was made in collaboration with Angela Luong.  Please visit the other awesome posts on their blog by going going here.

I/D #3

Inquiry Activity Summary
1.Today we will be looking at the devriation of the "identity". "Identity" is a proven facts and formula that is always proven true. For example, the pythagorean theoream of a^2+b^2=c^2 is an identity.

To begin with, the pythagorean theorem of a triangle using x, y, and r, is x^2+Y^2=r^2. To make it equal to 1, we would have to divide everything by r^2. Since the ratio for cosine on the  unit circle is x/r and the ratio for sine is y/r, we can say that cos^2theata+sine^2theata=1. Therefore, we can conclude that sin^2x+cos^2x=1 is a pythagorean identity because it is proven to be exactly the same as x/r^2+y/r^2=1. The replacement of x and y with cos and sin proves that it is true.

Another way that is proven true is to plug in the "magic 3" ordered pairs from the unit circle. When we plug in the pairs, we know that it is equal to 1. Therefore, it is an identity.

2. To derive the identity from sin^2+cos^2x=1, first divide everything by cos^2. Sin/tan is equal to tan. Because it is squared with an x, we leave that the same. Cos^2x/cos^2x is equal to 1. 1/cos^2x is equal to sec^2x

To derive it from cosecant and cotangent, you set up the same. Sin2^x+cos^2x=1. To begin with, you divide everything by sin^2x. Sin^2x/sin^2x=1. Cos^2x/sinx^2 is equal to cot^2x. 1/sin^2x is equal to csc^2x.

Inquiry Activity Reflection:

The connections that I see between Units N, O, P, and Q so far are unit circle has relation between these identities. These identities is basically derived from the pythagorean theorem. The pythagorean theorem can also derived from these triq functions.

If I had to describe trigonometry in THREE words, they would be identity, magic ordered pairs, and pythagorean theorem.

WPP #13 & 14: Unit P Concept 6 & 7

This WPP #13-14 was made in collaboration with Angela Luong. Please visit the other awesome posts on their blog by going here

Law of Sines: 

Amber is walking up the street 13 feet towards a store called "Frosty" due North of her car. Her friend sends her a text to get her a cupcake from the store "Cakes-galore!", the shop is located at a bearing of 046*; the "Frosty" store is located at a bearing of 135*. How far is each store from Amber? 

Law of Cosines: 

Amber is walking down to her new job at Clothing Express located 12 feet due North. She hears a cry of "Thief!" and turns her head 32* to see a man carrying a bag of money running 17 feet due East. Amber tries to run after him. How far is the man from Amber? 

BQ: Law of Sin and Area Formula

Law of Sin

To being with, we will be looking at the law of sin and how it is derived to get the actual formula. The law of sin begins with  a triangle. When it is cut through, it give us a hypotenuse.

In trigonometry, we know that sin is opposite over hypotenuse. Therefore, we know that the sin of angle A is equal to h over c. You multiply both sides by c to get h alone 

Next we must find the law of sin for angle C. Using soh-cah-toa the sin of angle C is h over a. We must isolate the h by multiplying a to get aSinC.

Finally we can use the transitive property to derived to find the real sin formula. You take the answers to both angle and set it equal to each other. Divide by ca to both side to get SinA over side a and SinC equals to side c. There, you get the toe ratio of the law of sin 

You can only use the law of sin if you have AAS(angle, angle, side), ASA(angle, side, angle), and SSA(side, side, angle).

The case when you cannot use the law of sin is when you don't know the opposite side or angle. For instance like in this picture it is given the side but the angle is missing. In addition to, the angle is also given but the opposite side is missing. 

4.Area Formula

The area of an oblique triangle is derived with a combination of the law of sin and a regular area of a triangle. You would use the same formula of 1/2 times based times height with the substitution of h. To find h, you use the law of sin, h is equal to aSinC. There, you have the devriation of the oblique triangle.  Also for it to be an a oblique triangle, all sided must be different.

There is a several different form of the area depending in the angles you are looking for.

Reference:

Math Warehouse

WPP #12: Unit O Concept 10: Solving angle of elevation and depression word problems

Christine and Jessica wanted to promote their newly open clothing shop. In order for potential customers to see the shop they decided to put a banner on the top of the clothing shop. Jessica is standing away from the building to check on the sign. The angle of elevation is 25.25 degress from jessica to the top where Christine is at. IF the base of the building is 350 ft from Jessic how high is the building?

After finishing up with the sign Christine wanted to use the latter down. She estimated the angle of depression of 30 degress at where she is now to where Christine is at. She is 200 ft higher than the base of the building. How long is her way down the building?

I/D#2: Unit O Concept 7-8: Deriving the pattern of SRT

Inquiry Activity Summary:

45,45,90 degrees SRT
To begin, we need to label each side equals to 1. Next, the equallateral needs to be cut in half in order to find the 45,45,90 degrees triangle. 

Since the given information is only 2 sides of the triangles, we need to find the missing sides. You can find the missing side by using the pythagorean theorem of a^2+b^2=c^2. The legs of the triangle will always A and B while the hypothenus is C. When it is plugged in, it should be (1)^2+(1)^2=C^2. After solving, you should get C= radical 2.

For it to be a SRT, N should be added to the pattern because the value can be change anytime. The final pattern of the 45,45,90 should be 1n,1n, and N radical 2. 

30,60,90 SRT

Now we are going to look at another special right triangle. It is the 30,60,90 degrees. To begin, we label each side equalss to 1. Then we cut the triangle in half.

Next, the 1 on the short leg becomes 1/2 because the triangle has been cut half. The hypotenus will stay as a value of 1. The pythagorean theoream needs to be use in order to find the other missing side of the triangle

The pythagorean theorem is a^2+b^2=c^2 After solving, you should get C=radical 3/2

Since the value of each side does not follow the pattern, we must find the pattern by multiplying everything by 2. 

Finally, we should get the pattern of 1,2,and radical 3. However, the n needs to be there because the value of these can be change depending on the triangle.

Inquiry Activity Reflection:

The coolest thing I learned from this activity was that we can pattern came from a triangle that has all side equals to 1.

The coolest thing I learned from this activity was I can derive the formula if I were to forget it during the test or in the future.

I/D#1 Concept 7: Deriving Unit Circle

In this activity, we are able to derive the unit circle from where it came from. The unit circle is formed by the 30,60,90 degrees and the 45,45,90 degrees triangle. We derive this by using the special right triangle formula.

Inquiry Activity Summary

  The hypotenuse is always labeled r. The verticle value is y and horizontal x. The value for the hypotenuse is 2, x value is radical 3 and the y value is 1. To make the hypotenuse equals to , divide everything by 2.

This triangle is the same, however the angle is in a different position. The x,y,r is label the same with the values. However, the ordered pairs will be in different.

The special right triangle of the 45,45,90 will have a different value. The label of the x,y and r will be the same. To derive it, we need to find the value of each angle. Since 90 degrees value is radical 2 and we want it equal to 1, we must divide everything by radical 2. Since the other angle is being divided by radical 2 we must rationalize it because the bottom can't have a radical number.

This activity help me derive the unit circle because the unit circle is basically made up of the special right triangles including the 45,45,90 degrees and 30,60,90 degrees.

The value of these triangle changed when it is drawn in the second, third, and fourth quadrant by the negative and positive signs

In the second quadrant it is still in the first half, which is positive but it is in the left side. Therefore the x value will be negative while the y value is positive.

The third quadrant is in the bottom half. Because it is on the bottom and to the left, both the x and y value will be negative

Finally, the value of the x and y in the fourth quadrant will be positive and negative. The x is positive and the y is negative because you are starting from the right side of the unit circle and going down.

Conclusion

The coolest thing I learn from this activity is that the unit circle is derive from the special right triangle

This activity will help me in this unit because I did not have to memorize a lot of thugs because I can work out the problems.

Something that I never realize about the special right triangle and the unit circle is that they are both related to each other in many ways