Point Continuity
Oscillating Behavior
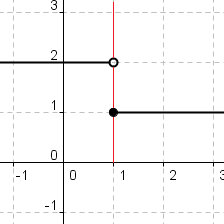
Jump Discontinuity
Infinite Discontinuity
2. A limit is the intended height of a function. It exist when there is an open hole on the graph. It is not the actual height but the intended height that it is trying to reach. The limit exist only when you reach the same height from both the left and right. A limit does not exist when there is a break in between the lines. For example in the jump discontinuity, a limit doe snot exist because it reaches two different places from left and right. A limit does not exist in the non removable discontinuities such as jump discontinuity, oscillating behavior, and infinite discontinuity. There is also a difference between the limit and value. A limit is the intended height while the value is the actual height. A value is represented by a closed circle.
Limits (intended height)
3. To evaluate the function numerically you have to set up the table and list the x value that is close to the number from left to right. You plug the equation onto the graphing calculator and trace the value. The y value will get closer and closer to the number therefore you can make ab educated guess of what the value is going to be. To evaluate it graphically you use your two finger and trace it from left to right. If the graph has a break then there is going to be a non removable type of discontinuity. To evaluate it numerically you first has to determine which kind of evaluation you're going to use. First. Start by using direct substitution. If it does not work you can determine it by using dividing out method, rationalizing, or limits at infinity
Limits Graphically
Limits Numerically
Credit/Disclaimer
Web Charter
Sage Math
All Math
Bakefield College
Khan Academy





No comments:
Post a Comment