Definition: a set of all point such that the difference in the distance from two point is constant.
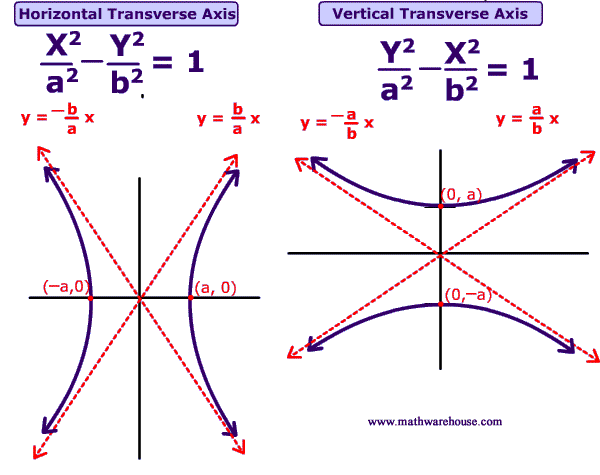
Algebraically: The equation is (x-h)^2 over a^2 minus (y-k)^2 over b^2 equals to 1.You can tell if the hyperbola is open left/right if x comes first. It will open up/down if y comes first in the equation. Also, the needs to be in standard form to make it easier to classify the hyperbola. The equation needs to be subtracted for it to be a hyperbola. Otherwise, it will be an ellipse.
Graphically: By looking at the hyperbola the x and the y affects how the graph will shape. It will shape the graph left/right, up/down. There will be a focus on one side and the vertex on the other side of the graph. The "C" will go through the focus while the transverse axis connect the two vertices together.The "a" and the "b" will affect where the two vertices and co vertices will be placed/ how much it will move on the graph.
Key: To start the equation needs to be in standard from which is (x-h)^2 over a^2 minus (y-k)^2 over b^2 equals to 1. The center could be find by taking the opposite of h and k from the standard form. From there, you can determine if it is up/down if y comes first and left/right if x comes first. To find "a" you take the square root of a^2. Similarly, you can find "b" by taking the square roots of b^2. Plot the center and count number of "a" from the center and "b" from the center to find the vertices and co vertices. The numbers that dominates in the ordered pairs will be the transverse axis and conjugate axis.You can use a^2+b^2=C^2 to find c. As for the eccentricity, you take C divided by A to get the answer. The two foci will be (x,y+-eccentricity). "The 'foci' of an hyperbola are 'inside of each branch and each focuses is located some fixed distance c from the center." (credit) Finally, to find the asymptote, you find the m slope by taking a/b or b/a depending on the direction of the branches. After finding the slope, plug in to y=mx+b .
Real World Application:
Hyperbola can be applied to the real world. For example, it could be the shape of your lamp, where it will cast a hyperbolic shape on your wall. It can also be found in many things such as Dulles Airports, sonic boom, cooling tower of nuclear reactors, stone in lake, etc.
Reference:
Picture Credit
Website Credit
Video Credit
RWA Example Credit
No comments:
Post a Comment