After finishing up with the sign Christine wanted to use the latter down. She estimated the angle of depression of 30 degress at where she is now to where Christine is at. She is 200 ft higher than the base of the building. How long is her way down the building?
Friday, March 7, 2014
WPP #12: Unit O Concept 10: Solving angle of elevation and depression word problems
Christine and Jessica wanted to promote their newly open clothing shop. In order for potential customers to see the shop they decided to put a banner on the top of the clothing shop. Jessica is standing away from the building to check on the sign. The angle of elevation is 25.25 degress from jessica to the top where Christine is at. IF the base of the building is 350 ft from Jessic how high is the building?
Wednesday, March 5, 2014
I/D#2: Unit O Concept 7-8: Deriving the pattern of SRT
Inquiry Activity Summary:
45,45,90 degrees SRT
To begin, we need to label each side equals to 1. Next, the equallateral needs to be cut in half in order to find the 45,45,90 degrees triangle.
Since the given information is only 2 sides of the triangles, we need to find the missing sides. You can find the missing side by using the pythagorean theorem of a^2+b^2=c^2. The legs of the triangle will always A and B while the hypothenus is C. When it is plugged in, it should be (1)^2+(1)^2=C^2. After solving, you should get C= radical 2.
For it to be a SRT, N should be added to the pattern because the value can be change anytime. The final pattern of the 45,45,90 should be 1n,1n, and N radical 2.
30,60,90 SRT
Now we are going to look at another special right triangle. It is the 30,60,90 degrees. To begin, we label each side equalss to 1. Then we cut the triangle in half.
Next, the 1 on the short leg becomes 1/2 because the triangle has been cut half. The hypotenus will stay as a value of 1. The pythagorean theoream needs to be use in order to find the other missing side of the triangle
The pythagorean theorem is a^2+b^2=c^2 After solving, you should get C=radical 3/2
Finally, we should get the pattern of 1,2,and radical 3. However, the n needs to be there because the value of these can be change depending on the triangle.
Inquiry Activity Reflection:
The coolest thing I learned from this activity was that we can pattern came from a triangle that has all side equals to 1.
The coolest thing I learned from this activity was I can derive the formula if I were to forget it during the test or in the future.
Saturday, February 22, 2014
I/D#1 Concept 7: Deriving Unit Circle
In this activity, we are able to derive the unit circle from where it came from. The unit circle is formed by the 30,60,90 degrees and the 45,45,90 degrees triangle. We derive this by using the special right triangle formula.
Inquiry Activity Summary
The hypotenuse is always labeled r. The verticle value is y and horizontal x. The value for the hypotenuse is 2, x value is radical 3 and the y value is 1. To make the hypotenuse equals to , divide everything by 2.
This triangle is the same, however the angle is in a different position. The x,y,r is label the same with the values. However, the ordered pairs will be in different.
The special right triangle of the 45,45,90 will have a different value. The label of the x,y and r will be the same. To derive it, we need to find the value of each angle. Since 90 degrees value is radical 2 and we want it equal to 1, we must divide everything by radical 2. Since the other angle is being divided by radical 2 we must rationalize it because the bottom can't have a radical number.
This activity help me derive the unit circle because the unit circle is basically made up of the special right triangles including the 45,45,90 degrees and 30,60,90 degrees.
The value of these triangle changed when it is drawn in the second, third, and fourth quadrant by the negative and positive signs
In the second quadrant it is still in the first half, which is positive but it is in the left side. Therefore the x value will be negative while the y value is positive.
The third quadrant is in the bottom half. Because it is on the bottom and to the left, both the x and y value will be negative
Finally, the value of the x and y in the fourth quadrant will be positive and negative. The x is positive and the y is negative because you are starting from the right side of the unit circle and going down.
Conclusion
The coolest thing I learn from this activity is that the unit circle is derive from the special right triangle
This activity will help me in this unit because I did not have to memorize a lot of thugs because I can work out the problems.
Something that I never realize about the special right triangle and the unit circle is that they are both related to each other in many ways
Tuesday, February 11, 2014
RWA#1: Unit M Concept 4-6 Conic Sections in real life
Hyperbola
Definition: a set of all point such that the difference in the distance from two point is constant.
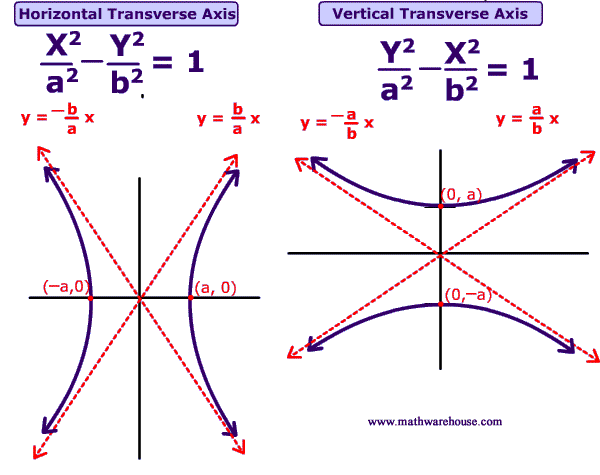
Algebraically: The equation is (x-h)^2 over a^2 minus (y-k)^2 over b^2 equals to 1.You can tell if the hyperbola is open left/right if x comes first. It will open up/down if y comes first in the equation. Also, the needs to be in standard form to make it easier to classify the hyperbola. The equation needs to be subtracted for it to be a hyperbola. Otherwise, it will be an ellipse.
Graphically: By looking at the hyperbola the x and the y affects how the graph will shape. It will shape the graph left/right, up/down. There will be a focus on one side and the vertex on the other side of the graph. The "C" will go through the focus while the transverse axis connect the two vertices together.The "a" and the "b" will affect where the two vertices and co vertices will be placed/ how much it will move on the graph.
Key: To start the equation needs to be in standard from which is (x-h)^2 over a^2 minus (y-k)^2 over b^2 equals to 1. The center could be find by taking the opposite of h and k from the standard form. From there, you can determine if it is up/down if y comes first and left/right if x comes first. To find "a" you take the square root of a^2. Similarly, you can find "b" by taking the square roots of b^2. Plot the center and count number of "a" from the center and "b" from the center to find the vertices and co vertices. The numbers that dominates in the ordered pairs will be the transverse axis and conjugate axis.You can use a^2+b^2=C^2 to find c. As for the eccentricity, you take C divided by A to get the answer. The two foci will be (x,y+-eccentricity). "The 'foci' of an hyperbola are 'inside of each branch and each focuses is located some fixed distance c from the center." (credit) Finally, to find the asymptote, you find the m slope by taking a/b or b/a depending on the direction of the branches. After finding the slope, plug in to y=mx+b .
Reference:
Picture Credit
Website Credit
Video Credit
RWA Example Credit
Definition: a set of all point such that the difference in the distance from two point is constant.
Algebraically: The equation is (x-h)^2 over a^2 minus (y-k)^2 over b^2 equals to 1.You can tell if the hyperbola is open left/right if x comes first. It will open up/down if y comes first in the equation. Also, the needs to be in standard form to make it easier to classify the hyperbola. The equation needs to be subtracted for it to be a hyperbola. Otherwise, it will be an ellipse.
Graphically: By looking at the hyperbola the x and the y affects how the graph will shape. It will shape the graph left/right, up/down. There will be a focus on one side and the vertex on the other side of the graph. The "C" will go through the focus while the transverse axis connect the two vertices together.The "a" and the "b" will affect where the two vertices and co vertices will be placed/ how much it will move on the graph.
Key: To start the equation needs to be in standard from which is (x-h)^2 over a^2 minus (y-k)^2 over b^2 equals to 1. The center could be find by taking the opposite of h and k from the standard form. From there, you can determine if it is up/down if y comes first and left/right if x comes first. To find "a" you take the square root of a^2. Similarly, you can find "b" by taking the square roots of b^2. Plot the center and count number of "a" from the center and "b" from the center to find the vertices and co vertices. The numbers that dominates in the ordered pairs will be the transverse axis and conjugate axis.You can use a^2+b^2=C^2 to find c. As for the eccentricity, you take C divided by A to get the answer. The two foci will be (x,y+-eccentricity). "The 'foci' of an hyperbola are 'inside of each branch and each focuses is located some fixed distance c from the center." (credit) Finally, to find the asymptote, you find the m slope by taking a/b or b/a depending on the direction of the branches. After finding the slope, plug in to y=mx+b .
Real World Application:
Hyperbola can be applied to the real world. For example, it could be the shape of your lamp, where it will cast a hyperbolic shape on your wall. It can also be found in many things such as Dulles Airports, sonic boom, cooling tower of nuclear reactors, stone in lake, etc.
Reference:
Picture Credit
Website Credit
Video Credit
RWA Example Credit
Thursday, January 16, 2014
WPP#10: Unit L Concepts 9-14 - Bsic Probabilities of Independent and or events
Create your own Playlist on LessonPaths!
WPP#9: Unit L Concept 4-8 - CAlculating Possibilities with Combinations and Permutations
Create your own Playlist on LessonPaths!
Monday, December 9, 2013
Unit K Concept 10: Writing repeating decimal as a rational
In this concept, student will learn about rational number. Students will be able to write the repeating decimal as a rational number without using a calculator. To solve for it, you need to use the sum of infinite geometric series. Students need to find the firs term and the common ratio. To get the common ratio. To find the common ratio, you take the number divided by the preceding number. Finally you plug into the formula and evaluate.
One thing that students need to be careful about it listing out the number. It will give you a completely different number if it is not listed right. Also students should be careful about subtracting the whole number by the fraction.
One thing that students need to be careful about it listing out the number. It will give you a completely different number if it is not listed right. Also students should be careful about subtracting the whole number by the fraction.
Subscribe to:
Posts (Atom)