I/D 4: Unit V

During the activities in class, we discussed  how the shapes would all fit into the graph. We think that if all of the shape is given, maybe we could fit it into the graph like a puzzle piece. For a perfectly shaped graph, it was easier to solve because the shape fit nicely into it. However, on other graphs, it is harder because the shape is not porportioned . In order to solve for the ones that are not perfect, we would have to estimate it by putting pieces subtract it by the amount that is not used. In addition to, we also look at the scale of the graph. To do that, can figure out an estimate by figuring out the area of each space. It will give you a good estimate of the area.  In conclusion, we think that the most accurate graph use is to fit the pieces of shape on to the graph and estimate. As for the area, we think that you can estimate by looking at the scale of the graph alone.

BQ #6: Unit U

1. A continuity is a function that is very predictable because it has no breaks, no holes, and no jumps. It can be drawn without lighting up a pencil, in a single, unbroken line. A continuity is in the removable discontinuity called the point discontinuity. On the other hand, a discontinuity is has all of the opposite characteristic of the continuity. It has a break, hole, and jump. The discontinuity is put into the categories of non-removable discontinuity. Types of non removable discontinuities are jump discontinuity, oscillating behavior, and infinite discontinuity. A jump discontinuity has is different from left/right and has a break between the lines. An  oscillating behavior is wiggly while infinite discontinuity has a vertical asymptote and unbounded behavior.

Point Continuity

Oscillating Behavior

Jump Discontinuity

Infinite Discontinuity

2. A limit is the intended height of a function. It exist when there is an open hole on the graph. It is not the actual height but the intended height that it is trying to reach. The limit exist only when you reach the same height from both the left and right. A limit does not exist when there is a break in between the lines. For example in the jump discontinuity, a limit doe snot exist because it reaches two different places from left and right. A limit does not exist in the non removable discontinuities such as jump discontinuity, oscillating behavior, and infinite discontinuity. There is also a difference between the limit and value. A limit is the intended height while the value is the actual height. A value is represented by a closed circle.

Limits (intended height)

3. To evaluate the function numerically you have to set up the table and list the x value that is close to the number from left to right. You plug the equation onto the graphing calculator and trace the value. The y value will get closer and closer to the number therefore you can make ab educated guess of what the value is going to be. To evaluate it graphically you use your two finger and trace it from left to right. If the graph has a break then there is going to be a non removable type of discontinuity. To evaluate it numerically you first has to determine which kind of evaluation you're going to use. First. Start by using direct substitution. If it does not work you can determine it by using dividing out method, rationalizing, or limits at infinity

Limits Graphically

Limits Numerically

Credit/Disclaimer
Web Charter
Sage Math
All Math
Bakefield College
Khan Academy

BQ #4: WHy is a "normal" tangent graph uphill, ut a "normal" tangent graph downhill?

An asymptote will occur in the graph if the triq function is undefined. It is undefined when x is equal to zero. Tangent is Y/X. The tangent graph will have an asymptote at some point when x is zero. The reason why tangent graph is uphill and some are downhill is because it follows the ASTC. In a tangent graph, Q1=positive, Q2=negative, Q3=positive and Q4=negative.

 It will go up/down depending on the asymptote. Cotangent graph will have a similar graph. It will still follow the ASTC however, cotangent and tangent have a different location of asymptote. Since cotangent is x/y, the asymptote will start at a different place. Boundaries in different place will lead to the graph to be uphill/downhill.

BQ #3: How do the graphs of sine and cosine relate to eatch of the others?

Sine and Cosine relates to Tangent whenever Cosine/X is equal to zero. It happens to be where the curve on the graph is at. The curve is based on the ASTC of Tangent. Therefore, it will have different curves depending on the ASTC.

Cotangent will have an asymptote whenever sine is equal to zero. When sine is equal to zero, you will have undefined answer, therefore have an asymptote. The graph is uphill/downhill depending on where the asymptote is placed at. In this situtation, asymptote is located at 0, Pi, and 2pi.

Secant is the reciprocal of cosine. Secant will have an asymptote whenever cosine is equal to zero. The asymptote will be at pi/2, 3pi/2. On the first curve, it goes up next to the asymptote because the recicprocal of a fraction will make the number big, therefore will have to increased the curve. The curve will touch the "mountain" based on ASTC however, it will never touch the asymptote.

Cosecant will have an asymptote whenever sine is equal to zero because cosecant is the reciprocal of sine. Sine is zero at 0, pi, 2pi. The curve will depend on the ASTC of Sine. Sine is positive in qudrant 1,2. Because of that, the graph will be above the x asix. In qudrant 3,4 sine is negative. The graph will be below the x axix and will get close to the asymptote.

BQ #5: Why Do Sine and Cosine not have Asymptote, but the other four triq graphs do??

Sine and Cosine not have asymptote because it will never be undefined. The triq function of sine is y/r and cosine x/r. Since r=1, sine and cosine will be never undefined.

 As for the other triq functions, it does have an asymptote because the x, y could equal to zero. Therefore, the triq value of these functions will be undefined. Undefined triq functions will always have an asymptote on the graph.

BQ #2: How do the Triq Graphs Relate to the United Circle?

A. Period? Why is the peirod for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

A period is the end and beginning of a cycle. It ends and starts when there is a repeating patterns. In this case. the reason why sine and cosine is 2 pi is because the pattern repeat itself fully around the Unit CIrcle. For tangent/cotangent, the pattern repeats only half way. For example in quadrant 1, tangent is positive, qudrant II negative, qudrant III positive, and quadrant IV negative. Therefore, it repeat itself only half of the graph.

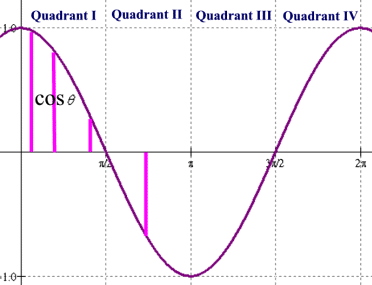
Below are the sign for the triq function. The patterns can be seen by looking at the sign from Qudrant I to Qudrant IV.

The graph below also demonstrates how the triq function of sine and cosine relates to the unit circle. It marks the period of a cycle of a pattern. It would take 2pi for sine and cosine to repeat.

B. How does the fact that sine and cosine have amplitudes of one (and the other triq functions don't have amplitudes) relate to what we know about the Unit Circle?

IT relates to what we  know about the Unit Circle because sine is between 1 and -1 while cosine is between -1 and 1. Therefore, there is no restriction for the other triq function.

Photo Credit/Disclaimer

Reflection#1: verifying triq function

24. Verifying is basically like a proof in geometry. You have to prove that the answer is proven true by solving. The differences between verifying identities and proof is that we have to use the identities to prove that something is true. 

25. Some tips and trick I think is help ful include listing all the steps and go through it one by one when you don't know where to start. Also it is important to do it carefully and not make simple mistake such as distributing negative.

26. The first step into verifying a triq function is to look at the problem that they give you. For example,You can tell if you have to foil if the function has a parenthesis. Another would be if you have a fraction. You can find the common denominator and solve. From there you have to use the identity and the basic rule of math to verify your function. The big key here is substitution. You have to use identity to prove/solve the triq function in order to simplify it to 1 function.